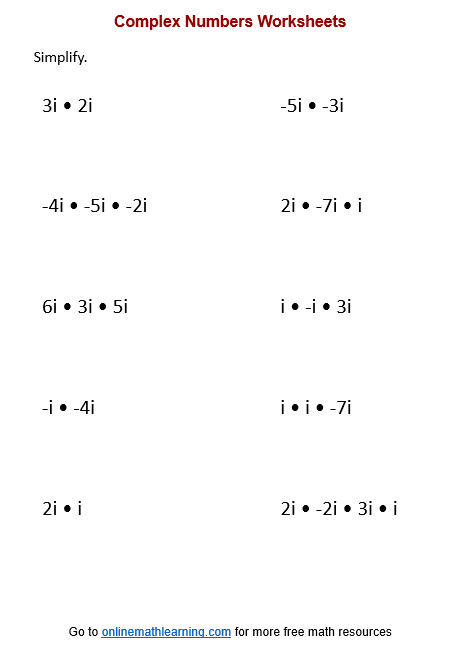
Examples, solutions, videos, and worksheets to help Algebra II students learn how to multiply complex numbers.
There are three sets of multiply complex numbers worksheets
In mathematics, the imaginary unit i is defined as the square root of -1. It is a fundamental concept in complex numbers. Powers of i repeat in a cyclic pattern, which makes them predictable. Here are the powers of i up to i 5 :
Multiply binomial complex numbers
To multiply binomial complex numbers, you use the distributive property of multiplication over addition.
Here’s how you multiply two complex numbers (a + bi) and (c + di)
Distribute each term in the first binomial to each term in the second binomial:
(a + bi) · (c + di)
= a · c + a · di + c · bi + bi · di
= ac + adi + bci + bdi 2
= ac + adi + bci - bd
= ac - bd + (ad + bc)i
Example:
Multiply (2 + 3i) by (1 − 4i):
Use the distributive property to multiply the terms:
(2 + 3i) · (1 − 4i)
= (2 · 1) + (2 · -4i) + (3i · 1) + (3i · - 4i)
= 2 - 8i + 3i - 12i 2
= 2 - 5i - (-12)
= 14 - 5i
Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Complex Number Worksheets.
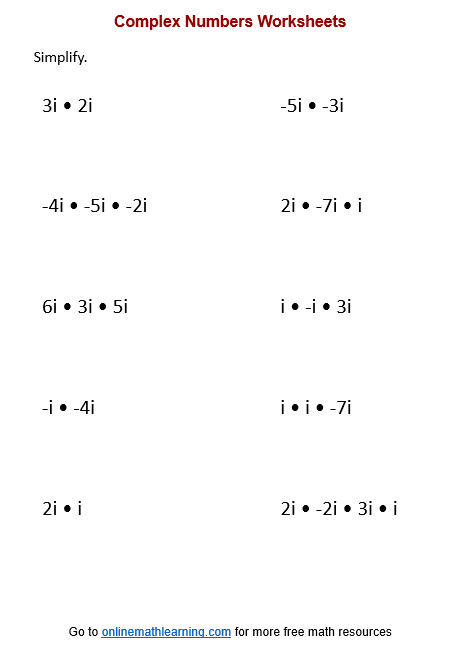

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.